

In this case, the final state of M would be q 2, which is not an accept state. The transitions would be the same up to step 6, where the transition function would be replaced with T( q 1, 0) q 2. Suppose that instead of the above example, we had fed in the string 10010. On any input string w, if the transition doesn't reach an accept state at the end of the input, it means that the machine rejects the input. accept because M is in accept state q 1at the end of the input. read 1, follow transition from q 1to q 1 ħ. read 1, follow transition from q 2to q 1 Ħ.

read 0, follow transition from q 1to q 2 ĥ. read 0, follow transition from q 0to q 1 Ĥ. read 1, follow transition from q 0to q 0 ģ.

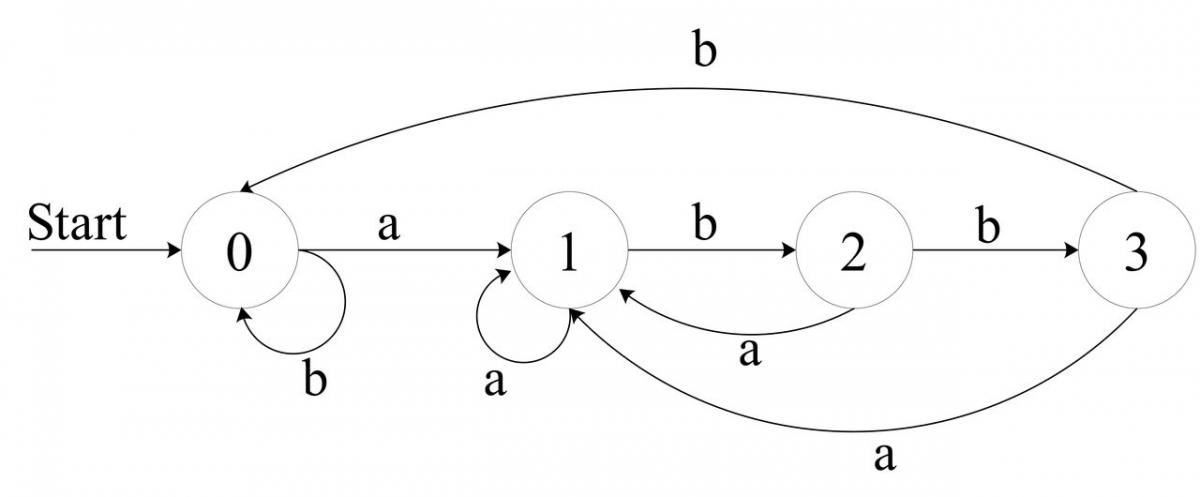
When the input string 10011 is fed to machine M, the processing proceeds as follows:Ģ. Practice ExercisesĬonsider the automaton (machine) M shown below. You can check this by comparing the transition table with the above state diagram. For instance if q 0 is the current state and 0 is the current input symbol, then the transition function is T( q 0, 0) q 1. The transition function can be represented as T(current state, current input symbol) next state. The transition function T can be described by a transitionfunction table, as follows: State/Input Symbol In this case, Q = and q 0is the start state. For instance, a finite automaton M is shown in the state diagram below. The operation of a finite-state automaton is always illustrated in a state diagram. For each pair of "current state" and "current input symbol" (the function input), the transition function produces as output the next state in the automaton. The transition function defines the movement of an automaton from one state to another by treating the current state and current input symbol as an ordered pair. Q 0 : the start state of the automaton, q 0 Q. : a finite set of input symbols, called alphabet. Q : a finite set of states the automaton can be in. It follows that f of S X Y is equal to f of f of S x.Application of Functions: Finite-State Automataĭefinition of A Finite-State Automaton | Languages Accepted by An AutomatonĪ finite-state automaton is comprised of a set of five objects ( Q,, q 0, F, T) where: 1. Why? Which is is at the Weber one to prove so it follows that statement is also true for why and therefore by structural induction. So it follows that this is also equal to f of if of s x w a again by definition f sorry of s X w a But again, this is seen as f of f of s x. Now we have that W and A are also both strings. And so, by the definition of the extended transition function, we also have This is going to be equal to f of f of S x, w a and we have buyer inductive step that this is going to be equal to f of yeah of f of s x w a.
Why, so you shouldn't statement is true in the case Where Why is the empty stream now for the inductive step? Let's suppose that why is the string which is the concatenation of W and a where w is a string in a is a letter? Now we're going to assume the statement is true for W As part of the inductive step, we're going to assume that f of S X W is equal to f of F s ex that will you You want to prove this statement is true For why so we have that f of s x y is equal to f A s X w a well, we have the x w is also a string. In this case, we have that f of yes x y It's going to be equal to F s ex Linda, which of course, is equal to F s ex in this is going to be equal to if of f of S x Landau, because we have that by the definition of extended transition function, f of s Lambda equals s and therefore we have This is equal to f of f of s X. So, first of all, well, let s be estate and X be a string and why be a string or the base step? Let's suppose that why is equal to Lambda the empty string. Now we'll prove that statement by structural induction, So we want to prove the ffs x y Z able to f of f of S X y. Autumn Aton and Rast e structural induction and the recursive definition of the extended transition function prove that extended transition function of f of S X Y is equal to they expended transition function If of the existing extended transition function effort s X Why for all states s and all strings ex and why? First of all, let's end the deterministic finance state Autumn Aton and let f be an extended transition function. Were given a deterministic finance state.


 0 kommentar(er)
0 kommentar(er)
